

The denominators of both terms can be factorised, like this:
Has two terms, both of which are rational expressions.

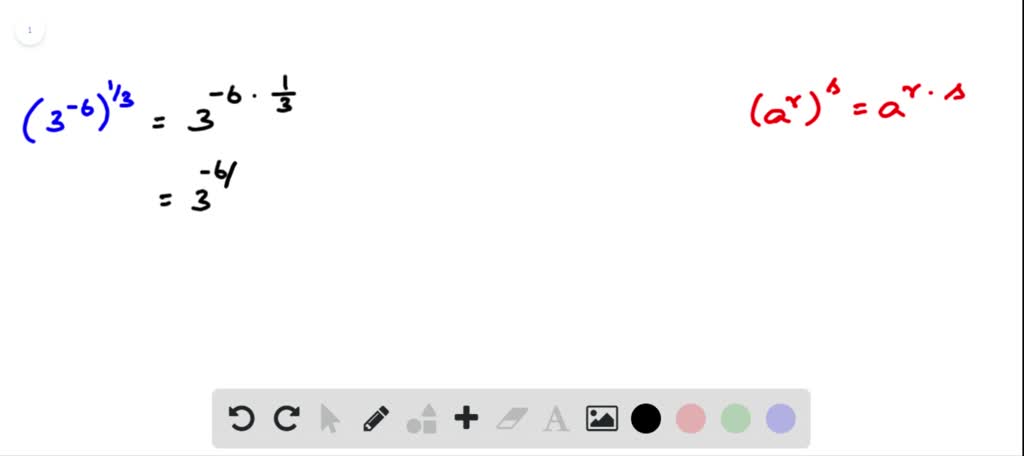
expand, simplify and factorise the numerator as necessary,.put all of the terms over a common denominator,.factorise the expression as much as possible without combining the terms into a single term,.If an expression contains more than one term, and one or more of the terms are rational expressions similar to that in example 2 above, then you will need to: The simplified form of the original expression is then: Now the expression can be simplified by cancelling the factor (m – 1) in both the numerator and denominator. Has the difference: ‘m² – m’ in the numerator, and the difference: ‘5m – 5’ in the denominator.īefore this expression can be simplified, both the numerator and denominator must be factorised, giving the following equivalent expression: This means that both the numerator and denominator of a rational expression must be expressed as a product of factors (ie ‘factorised’) before the expression can be simplified. Rational expressions are simplified by removing (also called ‘cancelling’) common factors that appear in both the numerator and denominator of the expression. Grouping like terms and simplifying we now have: If one or more terms of expression contain factors that are sums or differences in brackets, then the brackets may need to be removed by multiplication of factors before the expression can be simplified.įirst, the brackets must be expanded, like this:
#Simplifying expressions how to
How to simplify more difficult algebraic expressions.


 0 kommentar(er)
0 kommentar(er)
